This time I want to explore two problems I saw before while writing plugins for Binary Ninja. First problem, steaming from development of Annotator plugin (and I need to implement what I’ve learned here) and second is influenced by paper on Static Analysis and theory of lattices (if of course I’ve understood it correctly).
Problem 1: Walk the graph
Let’s say we want to track the state of a given variable in a program and all standard methods (get_rag_value_at(), SSA) don’t apply. Good example is Annotator plugin where I want to track instructions that influenced given variable (in that case - function argument) and not the value of expression itself. OK, I’m cheating a bit here in a sense that I haven’t yet tried SSA approach - more about that in next time. For now, let’s get back to our problem at hand.
In BinaryNinja blocks of a given function are available through an array. Let’s take a look at the example bellow
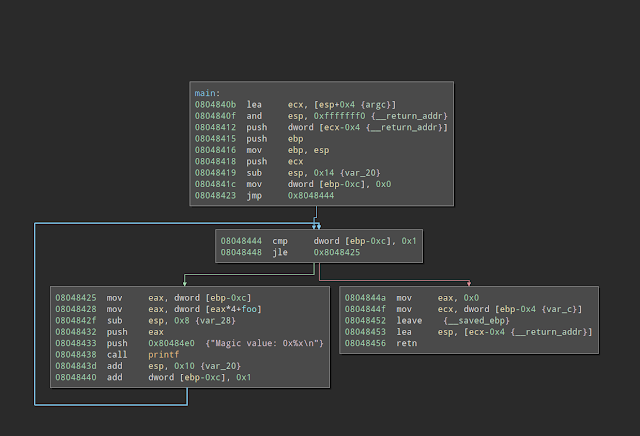
So now we access those blocks programmatically:
for block in current_function.basic_blocks:
print "%d -> %s"%(block.index+1, hex(block.start))
After running this code we get following result:
1 -> 0x804840bL
2 -> 0x8048450L
3 -> 0x8048435L
4 -> 0x8048455L
I guess you can see the problem right away. When we iterate over blocks we get them sequentially,but not exactly in the order that actual code might execute. Here, we will be processing blocks 2 and 3 after each other, while actually they will never be executed in the same code run (I’m assuming you are reading this in bright future where speculative execution bug was addressed once and for all). Truth be told, all functions parameters should be placed on the stack/in registers in the same block the function is being called, but there is absolutely no guarantee about that. I wasn’t sure about that so I’ve asked Gynvael, to which he responded - “well, for sure it will happen in the same function …”. Thanks buddy.
Fortunately it shouldn’t be that difficult to fix that. Well, for certain definition of fix.
def walk_graph(bv, function):
start = function.basic_blocks[0]
visited = []
walk(start, visited)
def walk(block, visited):
if block not in visited:
visited.append(block)
# Action here
for edge in block.outgoing_edges:
walk(edge.target, visited)
As you can see there is a simple recursive descent function tracking visited blocks. We are also taking advantage of nifty API feature where every block has incoming and outgoing edges that actually point to other blocks. So, does this work? Of course it does. Does it solve all problems? No and here is why. This code will work well for all functions with linear flow (with just conditional statements). Things get bit hairy when we introduce blocks with, what BinaryNinja calls back edges. In simple terms - loop statements.
Problem 2: Find all paths
So it happened - we hit the loop condition. Like one here

Checking blocks again…
1 -> 0x804840bL
2 -> 0x8048444L
3 -> 0x8048425L
4 -> 0x804844aL
If we use our recursive descent we get two paths: 1->2->3 and 1->2->4. We clearly see this is incorrect and reason for that is condition preventing from revisiting a block that we have already visited. We should be getting 1->2->4 and 1->[2->3->2]*->4 (simplified to 1->2->3->2->4). So, now we know, that blocks can be revisited. What shouldn’t be revisited? Of course, edges. Take a look a the code.
def all_paths(bv, function):
paths = []
first_block = function.basic_blocks[0]
for edge in first_block.outgoing_edges:
walk(edge, [], paths)
for path in paths:
print "---"
print "> %s "%path[0].source
for edge in path:
print "-> %s"%edge.target
def walk(edge, edges, paths):
if edge not in edges:
p_edges = copy.copy(edges)
p_edges.append(edge)
if len(edge.target.outgoing_edges):
for e in edge.target.outgoing_edges:
walk(e, p_edges, paths)
else:
paths.append(p_edges)
I think code explains itself pretty well, so there is no point linger too long around it. You might wonder why I’m making local copy of visited edges list. It is fairly simple - in the example bellow you can see that we branch in block 2 and one call stack of walk() is using edge 2->4 and later on, another call stack needs to take this edge again. If I keep single list of visited edges my search does terminate on block 2 missing last step of a path. Fun func: as I was told yesterday, and I blame my poor knowledge of CS I’ve just reinvented a variant of recursive DFS algorithm.
I have tested this code of relatively simple samples so if you have something more complex and it breaks horribly please let me know. Right now I’m just hoping someone will find it useful and I haven’t spent my evening doing poor’s man implementation of SSA. Well, only one way to find out. See you soon :)